欧拉公式的由来
在复数世界中,当我们集成三角表达式时,我们很可能会遇到所谓的欧拉公式。这个强大的方程式以传奇的数学家莱昂哈德·欧拉(Leonhard Euler)的名字命名。Euler公式,是Leonhard Euler的两个重要数学定理之一。在三角函数中使用的第一个公式,也称为欧拉恒等式,表示e i x = cos x + i sin x,其中e是自然对数的底数,而i是-1的平方根(请参阅 无理数)。当X是等于π或2π,式产生与π,2个优雅表达式ë,和我:ë我π= -1和ë 2我π = 1,分别。第二个也称为Euler多面体公式,是与任何多面体的面,顶点和边的数量相关的拓扑不变性(请参见 拓扑)。记为F + V = E + 2,其中F是面的数量,V是顶点的数量,E是边的数量。例如,一个立方体有6个面,8个顶点和12个边,并满足此公式。
我们将研究Euler公式如何使我们将复数表示为指数,并探索相对容易地建立复数的不同方法。
此外,我们还将考虑它的几种应用,例如欧拉恒等式的特殊情况,复数的指数形式,关键函数的替代定义以及de Moivre定理和三角可加恒等式的替代证明。
笔记:此Euler公式与其他Euler公式(例如凸多面体公式)有所区别。
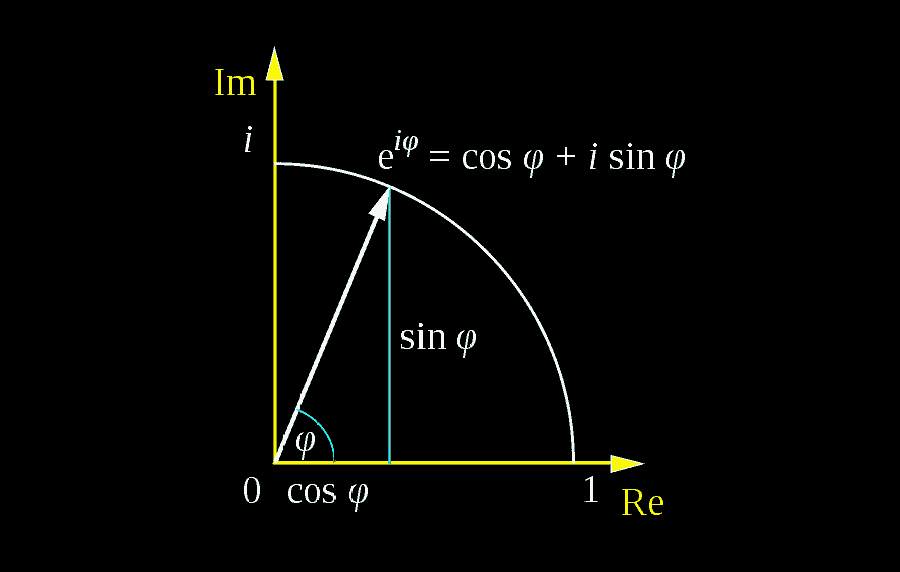
目录
欧拉公式的解释:简介,解释和示例
那么,欧拉公式到底是什么?简而言之,该定理表明:
e i x = cos x + i sin x
在哪里:
- X是一个实数。
- Ë是自然对数的底。
- 一世是虚数单位(即,的平方根)-1个)。
笔记
在此公式中,右侧有时缩写为 顺式X,尽管是左侧的表达式 Ë一世X 通常比 顺式 符号。
欧拉公式建立了三角函数和指数函数之间的基本关系。在几何上,可以将其视为在复平面中桥接相同单位复数的两个表示的一种方式。
让我们看一下Euler公式的一些关键值,并看一下它们如何对应于三角/单位圆中的点:
- 为了 X=0, 我们有 Ë0=cos0+一世罪0, 这使 1个=1个。到目前为止一切顺利:我们知道0 在三角圆上是 1个 在实轴上,这就是我们得到的结果。
- 为了 X=1个, 我们有 Ë一世=cos1个+一世罪1个。这个结果表明Ë一世精确地是单位圆上的角度为1弧度的点。
- 为了 X=π2个, 我们有 Ë一世π2个=cosπ2个+一世罪π2个=一世。该结果在与物理有关的某些计算中很有用。
- 为了 X=π, 我们有 Ë一世π=cosπ+一世罪π, 意思就是 Ë一世π=-1个。这个结果等同于著名的欧拉身份。
- 为了 X=2个π, 我们有 Ë一世(2个π)=cos2个π+一世罪2个π, 意思就是 Ë一世(2个π)=1个,与 X=0。
理解欧拉公式的关键在于如下重写公式:(Ë一世)X=罪X+一世cosX在哪里:
- 可以将右手表达式视为带角度的单位复数X。
- 左手表达式可以认为是将1弧度单位复数提高为X。
并且由于将单位复数提高为幂可以被视为重复的乘法(即,在这种情况下为相加角),因此欧拉公式可以解释为围绕单位圆到达同一点的两种不同方式。
派生
欧拉公式至少可以通过三种方式建立。一阶推导基于幂级数,其中指数,正弦和余弦函数作为幂级数展开,得出该公式确实成立。
欧拉公式的第二个推导基于微积分,其中将方程的两边都视为函数并进行相应的微分。然后,这导致了对公共属性的识别-可以利用该属性来表明两个功能确实相等。
欧拉公式的另一个推导涉及在复平面中使用极坐标,通过该极坐标可以得到[R 和 θ随后被发现。实际上,您仅通过查看公式本身就可以猜测这些值是什么!
派生1:功率系列
欧拉公式最直观的推导之一就是使用幂级数。它在于扩展指数,正弦和余弦的幂级数-最终得出等式成立的结论。
需要说明的是,这种方法假设幂级数展开式为 罪ž, cosž, 和 Ëž到处都是绝对收敛的(例如,它们适用于所有复数)ž)。但是,它还具有显示欧拉公式适用于所有复数的优点ž 也一样
对于复杂的变量 ž的幂级数展开的Ëž 是Ëž=1个+ž1个!+ž2个2个!+ž33!+ž44!+⋯现在,让我们来 ž 成为 一世X (在哪里 X是任意复数)。作为ž 被提升到越来越大的力量, 一世也被提升到越来越大的力量。该前八对权力的一世 看起来像这样:(根据定义 )一世0=1个一世4=一世2个⋅一世2个=1个一世1个=一世一世5=一世⋅一世4=一世一世2个=-1个(根据定义 一世)一世6=一世⋅一世5=-1个一世3=一世⋅一世2个=-一世一世7=一世⋅一世6=-一世(注意周期性的权力一世: 1个, 一世, -1个, -一世。我们将很快使用这些功能。)
和 ž=一世X,扩展 Ëž 变成:Ë一世X=1个+一世X+(一世X)2个2个!+(一世X)33!+(一世X)44!+⋯提取力量 一世,我们得到:Ë一世X=1个+一世X-X2个2个!-一世X33!+X44!+一世X55!-X66!-一世X77!+X88!+⋯并且自从幂级数展开以来 Ëž是绝对收敛的,我们可以在不改变其价值的情况下重新排列其条件。将实项和虚项组合在一起便得出:Ë一世X=(1个-X2个2个!+X44!-X66!+X88!-⋯)+一世(X-X33!+X55!-X77!+⋯)现在,让我们绕道而行,看看正弦 和 余弦的幂级数。电源系列cosX 是cosX=1个-X2个2个!+X44!-X66!+X88!-⋯而对于 罪X, 这是罪X=X-X33!+X55!-X77!+⋯换句话说,我们拥有的最后一个方程正好是Ë一世X=cosX+一世罪X这就是我们一直在寻找的欧拉公式的陈述。
推导2:微积分
建立欧拉公式的另一种巧妙方法是同时考虑两者 Ë一世X 和 cosX+一世罪X作为功能的X,然后区分它们以找到关于它们的一些共同属性。
为了做到这一点,必须假设这些功能 Ëž, cosX 和 罪X为所有实数定义和可区分X 和复数 ž。通过假设这些函数对于所有复数都是可微的,也有可能证明欧拉公式也适用于所有复数。
首先,让 F1个(X) 和 F2个(X) 是 Ë一世X 和 cosX+一世罪X, 分别。差异化 F1个然后通过链式规则得出:F1个′(X)=一世Ë一世X=一世F1个(X)同样,区别 F2个 还产生:F2个′(X)=-罪X+一世cosX=一世F2个(X)换句话说,两个函数都满足微分方程 F′(X)=一世F(X)。现在,考虑功能F1个F2个,这是对所有对象定义明确的X (自从 F2个(X)=cosX+一世罪X对应于单位圆上的点,永远不会为零)。解决之后,在该函数上使用商规则,将得出:(F1个F2个)′(X)=F1个′(X)F2个(X)-F1个(X)F2个′(X)[F2个(X)]2个=一世F1个(X)F2个(X)-F1个(X)一世F2个(X)[F2个(X)]2个=0由于这里的导数是 0,这意味着该功能 F1个F2个首先必须是一个常数。这个常数的值是多少?让我们通过插入来弄清楚X=0 进入功能:(F1个F2个)(0)=Ë一世0cos0+一世罪0=1个换句话说,我们必须所有人都拥有 X:(F1个F2个)(X)=Ë一世XcosX+一世罪X=1个在移动之后 cosX+一世罪X 在右边,成为我们一直在寻找的著名公式。
推导3:极坐标
欧拉公式的又一个巧妙的证明涉及将指数视为数字,或更具体地说,将其视为极坐标下的复数。
确实,我们已经知道,所有非零复数都可以以独特的方式在极坐标中表示。特别是任何形式的表格Ë一世X (与真实 X)(非零)可以表示为:Ë一世X=[R(cosθ+一世罪θ)在哪里 θ是它与正实轴的主角(例如,0≤θ<2个π), 和 [R是它的半径([R>0)。我们不对的值做任何假设[R 和 θ,但事实是它们是 X (可能包含也可能不包含 X作为变量)。它们将在证明过程中确定。
(但是,我们知道的是 X=0,左侧是 1个,这意味着 [R 和 θ满足初始条件的[R(0)=1个 和 θ(0)=0, 分别。)
对于什么是价值,我们将通过开始区分等式的两边。通过指数的定义,相对于X 产量 一世Ë一世X。在微分方程式的右边之后,方程式变为:一世Ë一世X=d[RdX(cosθ+一世罪θ)+[R(-罪θ+一世cosθ)dθdX我们正在寻找一种在以下方面具有独特性的表达方式: [R 和 θ。摆脱Ë一世X,我们换回 [R(cosθ+一世罪θ) 为了 Ë一世X 要得到:一世[R(cosθ+一世罪θ)=(cosθ+一世罪θ)d[RdX+[R(-罪θ+一世cosθ)dθdX到达那里后,分发 一世 然后在左侧产生:[R(一世cosθ-罪θ)=(cosθ+一世罪θ)d[RdX+[R(-罪θ+一世cosθ)dθdX分别将虚部和实部相等,我们得到:一世[Rcosθ=一世罪θd[RdX+一世[RcosθdθdX和-[R罪θ=cosθd[RdX-[R罪θdθdX我们在这里是一个系统,两个方程和两个未知数,其中d[R/dX 和 dθ/dX是变量。我们可以通过几个步骤解决它。首先,通过分配α 至 d[R/dX 和 β 至 dθ/dX,我们得到:(一世)(二)(一世)[Rcosθ=(罪θ)α+([Rcosθ)β(二)-[R罪θ=(cosθ)α-([R罪θ)β其次,将(I)乘以 cosθ 和(II)由 罪θ,我们得到:(三)(四)(三)[Rcos2个θ=(罪θcosθ)α+([Rcos2个θ)β(四)-[R罪2个θ=(罪θcosθ)α-([R罪2个θ)β这些操作的目的是消除 α 通过执行(III)–(IV),当我们这样做时,我们得到:[R(cos2个θ+罪2个θ)=[R(cos2个θ+罪2个θ)β自从 cos2个θ+罪2个θ=1个,出现了一个更简单的方程式:[R=[Rβ由于 [R>0 对所有人 X,这意味着 β -我们已经设定为 dθ/dX —等于 1个。
到达该位置后,将结果代入(I)和(II)并进行一些抵消,我们得到:0=(罪θ)α0=(cosθ)α这意味着 α -我们已经设定为 d[RdX —必须等于 0。
从事实 d[R/dX=0,我们可以推断出 [R必须是一个常数。同样,从事实dθ/dX=1个,我们可以推断出 θ=X+C 对于一些常数 C。
但是,由于 [R满足初始条件 [R(0)=1个,我们必须拥有 [R=1个。同样,因为θ 满足初始条件 θ(0)=0,我们必须拥有 C=0。那是,θ=X。
和 [R 和 θ 现在已经确定,我们可以将它们插入原始方程式并获得:Ë一世X=[R(cosθ+一世罪θ)=cosX+一世罪X正如预期的那样,这正是欧拉实数公式的陈述 X。
应用领域
作为数学中最重要的方程式之一,欧拉公式无疑在不同主题中都有其有趣的应用领域。其中包括:
- 著名的欧拉身份
- 复数的指数形式
- 三角函数和双曲函数的替代定义
- 将指数和对数函数推广为复数
- de Moivre定理和三角可加恒等式的替代证明
欧拉的身份
欧拉的恒等式通常被认为是数学中最美丽的方程式。它写为
Ë一世π+1个=0
它展示了数学中最重要的五个常数。这些都是:
- 该添加剂的身份 0
- 该统一 1个
- 该丕恒 π (圆的周长与其直径之比)
- 的自然对数的基地 Ë
- 的虚数单位 一世
其中,代表三种类型的数字:整数,无理数和虚数。还表示了三个基本的数学运算:加法,乘法和乘幂。
我们从欧拉公式开始获得欧拉的身份Ë一世X=cosX+一世罪X并通过设置 X=π 并发送后续 -1个到左侧 中间形式Ë一世π=-1个在复平面中的三角单位圆的上下文中是常见的:它对应于单位圆上相对于正实轴的角度为π。
指数形式的复数
至此,我们已经知道复数 ž可以用笛卡尔坐标表示为X+一世ÿ, 在哪里 X 和 ÿ 分别是的实部和虚部 ž。
实际上,相同的复数也可以用极坐标表示为[R(cosθ+一世罪θ), 在哪里 [R 是它到原点的距离的大小,并且 θ 是它相对于正实轴的角度。
但这还不止于此:由于有了欧拉公式,现在每个复数都可以表示为复指数 ,如下所示:
ž=[R(cosθ+一世罪θ)=[RË一世θ
在哪里 [R 和 θ 与以前的数字相同。
从 (X,ÿ) 至 ([R,θ),我们使用公式[R=X2个+ÿ2个θ=阿坦2(ÿ,X)(在哪里 阿坦2(ÿ,X)是两个参数的反正切函数与阿坦2(ÿ,X)=Arctan(ÿX) 每当 X>0)
反之,从 ([R,θ) 至 (X,ÿ),我们使用以下公式:X=[Rcosθÿ=[R罪θ复数的指数形式也使得乘以复数容易得多-就像同样的方式直角坐标使另外更容易。例如,给定两个复数ž1个=[R1个Ë一世θ1个 和 ž2个=[R2个Ë一世θ2个,我们现在可以将它们相乘,如下所示:ž1个ž2个=[R1个Ë一世θ1个⋅[R2个Ë一世θ2个=[R1个[R2个Ë一世(θ1个+θ2个)本着同样的精神,我们还可以将两个相同的数字除以如下:ž1个ž2个=[R1个Ë一世θ1个[R2个Ë一世θ2个=[R1个[R2个Ë一世(θ1个-θ2个)
笔记
可以肯定的是,这些确实以指数的属性为前提,例如Ëž1个+ž2个=Ëž1个Ëž2个 和 Ë-ž1个=1个Ëž1个,例如可以通过扩展 Ëž1个, Ë-ž1个 和 Ëž2个。
如果我们使用矩形 X+一世ÿ取而代之的是,相同的除法将需要乘以分子和分母中的复共轭。对于极坐标,情况将是相同的(可能更糟)。
如果有的话,指数形式肯定可以使我们更容易看到,将两个复数相乘与将幅度相乘和相加角实际上是相同的,将两个复数相除与将幅度相乘并相减得出的角确实相同。
关键功能的替代定义
欧拉公式还可用于为关键函数(例如复数指数函数),三角函数(例如正弦,余弦和正切)及其双曲线对应项提供替代定义。它也可以用来建立这些功能之间的关系。
复指数函数
首先,回想一下欧拉的公式指出Ë一世X=cosX+一世罪X如果假定该公式对实数成立 X仅指数函数才定义为虚数。但是,我们还可以通过简单的技巧将指数函数扩展为包括所有复数:
Ëž=ËX+一世ÿ(=ËXË一世ÿ)=dFËX(cosÿ+一世罪ÿ)
笔记
在这里,我们不必假设指数的加法属性成立(确实如此),而是第一个表达式和最后一个表达式相等。
换句话说,复数的指数 X+一世ÿ只是其数量级为的复数ËX谁的角度是ÿ。有趣的是,这意味着复指数本质上将垂直线映射到圆。这是说明这一点的动画:
三角函数
除了扩展指数函数的域外,我们还可以使用欧拉公式为反角导出相似的方程 -X:Ë-一世X=cosX-一世罪X该方程式与Euler公式本身一起构成了一个方程式系统,我们可以从中分离出正弦函数和余弦函数。
例如,通过减去 Ë-一世X 来自的等式 Ë一世X 等式,余弦抵消并除以 2个一世,我们得到正弦函数的复杂指数形式:
罪X=Ë一世X-Ë-一世X2个一世
同样,通过将两个方程式相加,可消除正弦并除以 2个,我们得到余弦函数的复杂指数形式:
cosX=Ë一世X+Ë-一世X2个
可以肯定的是,下面的视频更详细地说明了相同的派生。
另一方面,切线函数定义为罪XcosX,因此就复杂的指数而言,它变为:
棕褐色X=Ë一世X-Ë-一世X一世(Ë一世X+Ë-一世X)
如果证明欧拉公式对所有复数都成立(就像我们通过幂级数在证明中所做的那样),那么这三个公式也同样适用。它们的存在使我们可以在三角函数和复杂指数之间自由切换,这在计算导数和积分时是一个很大的优势。
双曲函数
除了三角函数外,双曲函数是可以根据复指数定义的另一类函数。实际上,通过这种连接,我们可以识别与三角函数相对应的双曲函数。
例如,从复杂的正弦和复杂的余弦开始,然后插入一世ž (并利用以下事实 一世2个=-1个 和 1个/一世=-一世), 我们有:罪一世ž=Ë一世(一世ž)-Ë-一世(一世ž)2个一世=Ë-ž-Ëž2个一世=一世(Ëž-Ë-ž2个)=一世辛žcos一世ž=Ë一世(一世ž)+Ë-一世(一世ž)2个=Ëž+Ë-ž2个=柯什ž从这些,我们也可以插入 一世ž进入复杂的切线并得到:棕褐色(一世ž)=罪一世žcos一世ž=一世辛ž柯什ž=一世谭ž简而言之,这意味着我们现在可以根据三角函数来定义双曲函数,如下所示:
辛ž=罪一世ž一世柯什ž=cos一世ž谭ž=棕褐色一世ž一世
但是,这些并不是我们可以提供新定义的唯一功能。实际上,根据欧拉公式,复数对数和一般复数指数是我们可以定义的另外两类函数。
复数对数和一般复数指数
与实数的对数相比,复数的对数表现出特殊的行为。更具体地说,它具有无限数量的值而不是一个。
为了了解如何操作,我们首先将对数函数定义为指数函数的逆函数。那是:Ëlnž=žln(Ëž)=ž此外,我们还知道对于任何复数对 ž1个 和 ž2个,指数的加法性质为:Ëž1个Ëž2个=Ëž1个+ž2个因此,当将非零复数表示为指数时,我们具有:ž=|ž|Ë一世ϕ=Ëln|ž|Ë一世ϕ=Ëln|ž|+一世ϕ在哪里 |ž| 是的大小 ž 和 ϕ 是的角度 ž从正实轴开始。而且由于对数只是数字的指数,当对数升为Ë,以下定义是按顺序进行的:lnž=ln|ž|+一世ϕ首先,这似乎是定义复数对数的一种可靠方法。但是,再看一遍,则发现以这种方式定义的对数可以采用无限数量的值-这是因为ϕ 也可以选择其他任意形式的形式 ϕ+2个πķ (在哪里 ķ 是一个整数)。
例如,我们从较早的时候已经看到 Ë0=1个 和 Ë2个π一世=1个。这意味着可以定义1个 两者都 0 和 2个π一世 —或任何形式的表格 2个πķ一世 为此(在哪里 ķ 是一个整数)。
为了解决这个难题,通常使用两种单独的方法。第一种方法是简单地将复数对数视为一个多值函数。即,将每个输入映射到一组值的函数。实现此目的的一种方法是定义lnž 如下:{ln|ž|+一世(ϕ+2个πķ)}在哪里 -π<ϕ≤π 和 ķ是一个整数。在这里,该子句-π<ϕ≤π 具有限制角度的作用 ž仅限一位候选人。因此,ϕ以这种方式定义通常被称为主角度的ž。
第二种方法(可以说更优雅)是简单地定义的复数对数。 ž 以便 ϕ 是...的主角 ž。有了这样的理解,原始的定义便变得清晰起来:
lnž=ln|ž|+一世ϕ
例如,根据这一新规则,我们将拥有 ln1个=0 和 ln一世=ln(Ë一世π2个)=一世π2个。我们不再受制于角度周期性的问题!
但是,由于限制 -π<ϕ≤π,复数对数的范围现在减小到矩形区域 -π<ÿ≤π(即主体分支)。而且,如果我们想保留对数与指数之间的逆关系,我们还需要对指数函数的域进行同样的处理。
但是,由于复数对数现已定义明确,因此我们也可以基于它定义许多其他内容,而不会产生歧义。这样的例子就是通用复数指数(基数为非零)一种),其定义如下:
一种ž=Ëln(一种ž)=dFËžln一种
例如,使用上面定义的一般复指数,我们现在可以了解 一世一世 实际上意味着:一世一世=Ë一世ln一世=Ë一世π2个一世=Ë-π2个≈0.208
De Moivre定理和三角可加恒等式的交替证明
该定理称为de Moivre定理,该定理指出:
(cosX+一世罪X)ñ=cosñX+一世罪ñX
在哪里 X 是一个实数, ñ是一个整数。默认情况下,通过归纳可以证明这是正确的(通过使用某些三角恒等式),但是借助欧拉公式,现在存在一个更简单的证明。
首先,请记住,指数的乘性表示(Ëž)ķ=Ëžķ虽然此属性通常不适用于复数,但在以下情况下确实适用: ķ是一个整数。确实,不难发现在这种情况下,数学本质上可以归结为对指数的加性的重复应用。
解决了这些问题之后,我们可以轻松得出de Moivre定理,如下所示:(cosX+一世罪X)ñ=(Ë一世X)ñ=Ë一世ñX=cosñX+一世罪ñX在实践中,这个定理是常用的寻找根复数的,并获得封闭形式表达的罪ñX 和 cosñX。通过将升为高阶的函数简化为简单的三角函数,可以做到这一点-从而可以轻松进行计算。
实际上,de Moivre定理不是唯一可以通过Euler公式简化证明的定理。其他身份,如添加剂的身份为罪(X+ÿ) 和 cos(X+ÿ),也可以从该效果中受益。
确实,我们已经知道 X 和 ÿ:cos(X+ÿ)+一世罪(X+ÿ)=Ë一世(X+ÿ)=Ë一世X⋅Ë一世ÿ=(cosX+一世罪X)(cosÿ+一世罪ÿ)=(cosXcosÿ-罪X罪ÿ)+一世(罪Xcosÿ+cosX罪ÿ)到达那里后,将两边的实部和虚部相等,然后得出我们一直在寻找的著名身份:
cos(X+ÿ)=cosXcosÿ-罪X罪ÿ罪(X+ÿ)=罪Xcosÿ+cosX罪ÿ
结论
从上面可以看出,欧拉公式是数学领域中不可多得的瑰宝。它建立了指数函数和三角函数之间的基本关系,并为复数,复函数和相关理论的世界发展铺平了道路。
的确,无论是欧拉的身份还是复数,欧拉的公式似乎始终如一 罪, 一世 和 Ë参与其中。这是一个功能强大的工具,精通它会带来巨大的回报,因此,它是“数学中最杰出的公式”的正确候选者。
| 描述 | 陈述 |
|---|---|
| 欧拉公式 | Ë一世X=cosX+一世罪X |
| 欧拉的身份 | Ë一世π+1个=0 |
| 复数(指数形式) | ž=[RË一世θ |
| 复指数 | ËX+一世ÿ=ËX(cosÿ+一世罪ÿ) |
| 正弦(指数形式) | 罪X=Ë一世X-Ë-一世X2个一世 |
| 余弦(指数形式) | cosX=Ë一世X+Ë-一世X2个 |
| 切线(指数形式) | 棕褐色X=Ë一世X-Ë-一世X一世(Ë一世X+Ë-一世X) |
| 双曲正弦(指数形式) | 辛ž=罪一世ž一世 |
| 双曲余弦(指数形式) | 柯什ž=cos一世ž |
| 双曲正切(指数形式) | 谭ž=棕褐色一世ž一世 |
| 复数对数 | lnž=ln|ž|+一世ϕ |
| 一般复杂exponentia升 | 一种ž=Ëžln一种 |
| 迪莫夫定理 | (cosX+一世罪X)ñ=cosñX+一世罪ñX |
| 正弦的加法标识 | 罪(X+ÿ)=罪Xcosÿ+cosX罪ÿ |
| 余弦的加法标识 |
资料来源
- 物理学家的数学(Susan M. Lea)
- 剑桥物理学公式手册(Graham Woan)












